
Perlin Noise Functions Support
The Fractal Science Kit fractal generator Perlin Noise Functions are associated with the PerlinNoise object:
Object PerlinNoise {
Amplitude0
Frequency0
AmplitudeFactor
FrequencyFactor
Octaves
}
Amplitude0 and Frequency0 define the initial amplitude and frequency to use when computing noise. AmplitudeFactor and FrequencyFactor are the factors applied to the amplitude and frequency within the noise iteration. Octaves is the number of iterations to use.
The following example illustrates how you would define a PerlinNoise object using the object's constructor:
PerlinNoise noise = PerlinNoise( \
Amplitude0, \
Frequency0, \
AmplitudeFactor, \
FrequencyFactor, \
Octaves \
)
This example assigns a noise object to the variable noise. The noise object is defined by the arguments: Amplitude0, Frequency0, AmplitudeFactor, FrequencyFactor, and Octaves, passed to the constructor.
Complex PerlinNoise.Apply(
PerlinNoise noise,
NoiseFunction,
NoiseOffset,
NoiseRotation,
NoiseFactor,
NoiseAbs,
z
)
Complex PerlinNoise.Apply3D(
PerlinNoise noise,
NoiseFunction,
NoiseOffset,
NoiseRotation,
NoiseFactor,
NoiseAbs,
z,
depth
)
These functions generate noise based on the given arguments. Each function returns a value between -1 and 1, inclusive. noise is a PerlinNoise object that controls the noise generation algorithm. NoiseFunction is 1 of the values given by the NoiseFunctions enum:
enum NoiseFunctions {
F0, "N(z)"
F1, "Sin(z.x * Factor + N(z))"
F2, "Sin(z.x * Factor + N(z) + Sin(z.y * Factor))"
F3, "Sin(z.x * Factor + N(z)) * Sin(z.y * Factor + N(z))"
}
NoiseFunction defines a function applied to the generated noise N(z) as given in the NoiseFunctions enum. NoiseOffset is an offset into the noise pattern and NoiseRotation is a rotation factor used to rotate the noise pattern. NoiseFactor is used for the Factor in all but the 1st of the noise functions. NoiseAbs is a Boolean that controls whether we sum the noise (NoiseAbs=False) or the absolute value of the noise (NoiseAbs=True) in the noise iteration. z is the point at which to compute the noise value. depth is the 3rd dimension required for 3D noise calculations.
Example:
global:
const PerlinNoise noise = PerlinNoise( \
Amplitude0, \
Frequency0, \
AmplitudeFactor, \
FrequencyFactor, \
Octaves \
)
finalize:
alternatePoint.Value = PerlinNoise.Apply( \
noise, \
NoiseFunction, \
NoiseOffset, \
NoiseRotation, \
NoiseFactor, \
NoiseAbs, \
pixel \
)
properties:
#include PerlinNoiseOptions
This example illustrates how an Alternate Value program can use the noise function PerlinNoise.Apply to set the alternate point Value to a noise value generated from the associated pixel. The properties section includes the PerlinNoiseOptions to allow the user to control the noise parameters used in the PerlinNoise constructor and the PerlinNoise.Apply function. This is typical for programs that use noise.
The following properties page is the result:
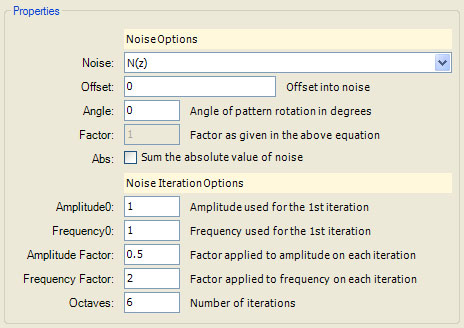
The PerlinNoiseOptions are defined in the built-in macros but are included here for reference:
#define PerlinNoiseIterationOptions
divider {
caption = "Noise Iteration Options"
}
option Amplitude0 {
type = Float
caption = "Amplitude0"
details = "Amplitude used for the 1st iteration"
default = 1
range = (0,)
}
option Frequency0 {
type = Float
caption = "Frequency0"
details = "Frequency used for the 1st iteration"
default = 1
range = (0,)
}
option AmplitudeFactor {
type = Float
caption = "Amplitude Factor"
details = "Factor applied to amplitude on each iteration"
default = 0.5
range = (0,1)
}
option FrequencyFactor {
type = Float
caption = "Frequency Factor"
details = "Factor applied to frequency on each iteration"
default = 2
range = (1,)
}
option Octaves {
type = IntegerEnum(1,8)
caption = "Octaves"
details = "Number of iterations"
default = 6
}
#end
#define PerlinNoiseOptions
divider {
caption = "Noise Options"
}
enum NoiseFunctions {
F0, "N(z)"
F1, "Sin(z.x * Factor + N(z))"
F2, "Sin(z.x * Factor + N(z) + Sin(z.y * Factor))"
F3, "Sin(z.x * Factor + N(z)) * Sin(z.y * Factor + N(z))"
}
option NoiseFunction {
type = NoiseFunctions
caption = "Noise"
default = NoiseFunctions.F0
size = Large
}
option NoiseOffset {
type = Complex
caption = "Offset"
details = "Offset into noise"
default = 0
}
option NoiseAngle {
type = Float
caption = "Angle"
details = "Angle of pattern rotation"
default = 0
range = [-360,360]
}
option NoiseFactor {
type = Float
caption = "Factor"
details = "Factor as given in the above equation"
default = 1
enabled = NoiseFunction <> NoiseFunctions.F0
}
option NoiseAbs {
type = Boolean
caption = "Abs"
details = "Sum the absolute value of noise"
default = False
}
constants {
NoiseRotation = Cis(DegreeToRadian(NoiseAngle))
}
#include PerlinNoiseIterationOptions
#end
Low-Level Noise Functions
The functions PerlinNoise.Apply and PerlinNoise.Apply3D are defined in the built-in macros using the low-level noise functions defined in this section. These low-level noise functions can be used directly if you need to define additional noise functions.
Complex PerlinNoise.Sum2D(PerlinNoise noise, z)
Complex PerlinNoise.SumAbs2D(PerlinNoise noise, z)
Complex PerlinNoise.Sum3D(PerlinNoise noise, z, depth)
Complex PerlinNoise.SumAbs3D(PerlinNoise noise, z, depth)
PerlinNoise.Sum2D takes a noise descriptor and a point z, and returns a value between -1 and 1, inclusive. PerlinNoise.SumAbs2D takes a noise descriptor and a point z, and returns a value between 0 and 1, inclusive.
PerlinNoise.Sum3D takes a noise descriptor, a point z, and a depth, and returns a value between -1 and 1, inclusive. PerlinNoise.SumAbs3D takes a noise descriptor, a point z, and a depth, and returns a value between 0 and 1, inclusive.
For detailed information about the algorithms and history of Perlin noise, see:
"Making Noise."
A set of slides by Ken Perlin.
"Perlin noise."
From Wikipedia, the free encyclopedia.
From Wikipedia, the free encyclopedia.