Mandelbrot / Julia / Newton

Home • Gallery • Tutorials • Download • Purchase • Site Map

Mandelbrot / Julia / Newton Properties Page

The Fractal Science Kit fractal generator Mandelbrot / Julia / Newton page holds a set of properties specific to Mandelbrot fractals and is visible only if the Fractal Type on the General page is set to Mandelbrot / Julia / Newton.

Mandelbrot / Julia / Newton

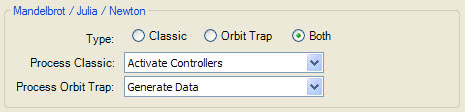
Fractal Science Kit - Mandelbrot / Julia / Newton Properties

The Mandelbrot / Julia / Newton section is used to select the Type of processing required for the Mandelbrot fractal. You can select Classic (non-orbit trap) processing, Orbit Trap processing, or Both. If Both is selected, the Process Classic and Process Orbit Trap controls are enabled and you can choose Generate Data or Activate Controllers for either property based on your requirements. Generate Data generates the sample data but does not enable the associated color controllers. Activate Controllers both generates the sample data and enables the associated color controllers.

Typically, you will set Type to either Classic or Orbit Trap. These are the most efficient settings since they eliminate any processing required solely for the other setting. You should choose Both only if you want to overlay the orbit traps on top of the classic display or if you need the data produced by both of the processing subsystems; e.g., you want to color the orbit traps using the sample's Magnitude (generated by the classic subsystem).

To overlay the orbit traps on top of the classic display, set both Process Classic and Process Orbit Trap controls Activate Controllers. When you process the fractal, trapped points are handled by the Orbit Trap Controllers and the non-trapped points are handled by the Classic Controllers. In truth, even trapped points are handled by the Classic Controllers if the orbit traps are partially transparent. That is, for each sample point, if the point was trapped by 1 or more orbit traps, the sample is passed to the Orbit Trap Master Controller for processing. If the color returned from the controller has an Alpha value less than 1 (i.e., it is partially transparent), the sample is passed to the Classic Master Controller and the result is used to fill the remaining space in the color. If the point was not trapped, the sample is passed directly to the Classic Master Controller for processing. Finally, any space remaining in the color is filled with the background color unless the Background's Visible property is not checked.

Alternatively, you may want to generate both Classic and Orbit Trap sample data, but handle the sample to color mapping using just the Orbit Trap Controllers or just the Classic Controllers. In these cases, you set the Type of processing to Both, and set Process Classic to Generate Data, and Process Orbit Trap to Activate Controllers, or vice versa.

Orbit Generation

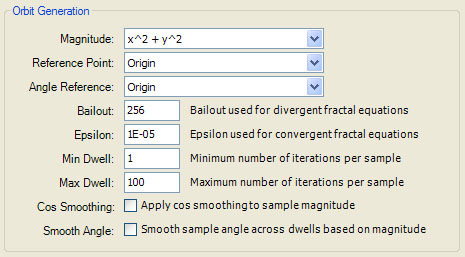
Fractal Science Kit - Mandelbrot / Julia / Newton Properties Orbit Generation

The Orbit Generation section of the page defines several properties that control the fractal iteration and some of the data associated with the orbit generation. The Magnitude and Reference Point are combined to calculate the magnitude used to terminate the fractal iteration. A vector is formed from the Reference Point to the current orbit point and the Magnitude distance metric is applied to the vector to obtain the magnitude. Divergent fractals terminate the iteration when the magnitude exceeds the Bailout value. Convergent fractals terminate the iteration when the magnitude is less than the value Epsilon. Convergent or Divergent fractals terminate the iteration when either condition occurs. The type of the fractal (Divergent, Convergent, or Convergent or Divergent) is set on the Fractal Equation page.

During the iteration, the orbit points are examined and the orbit is terminated early if the orbit point becomes NaN (Not a Number) usually indicating an error condition or an undefined operation was performed (e.g., 0/0).

The Reference Point is set to one of the following values:

Origin
Previous Orbit Point
Previous Magnitude, Current Angle
Previous Angle, Current Magnitude

Origin is the origin of the complex plane (i.e., the point 0+0i). Previous Orbit Point is the point prior to current point in the orbit. Previous Magnitude, Current Angle is the point on the vector from the origin to the current orbit point, whose magnitude is the distance from the origin to the previous orbit point. That is, it is the point with polar coordinates R=Abs(zprev1), Theta=Arg(z), where zprev1 is the previous orbit point and z is the current orbit point. Previous Angle, Current Magnitude is the point on the vector from the origin to the previous orbit point, whose magnitude is the distance from the origin to the current orbit point. That is, it is the point with polar coordinates R=Abs(z), Theta=Arg(zprev1).

Only Divergent fractals use Reference Point set to Origin. Convergent fractals or Convergent or Divergent fractals with Reference Point set to Origin, use Previous Orbit Point instead.

The Magnitude distance metric is set to one of the following values:

x^2 + y^2
x^2
y^2
Min( x^2, y^2 )
Max( x^2, y^2 )
Min( |x|, |y| )
Max( |x|, |y| )
( |x| + |y| )^2
( |x| - |y| )^2
| |x| + |y| |
| |x| - |y| |
| |x^3| + |y^3| |
| |x^3| - |y^3| |
| x^2 - y^2 |
| x * y |
| x^2 + y^2 + 2 * x * y |
| x^2 + y^2 - 2 * x * y |
| x^2 + y^2 + |2 * x * y| |
| x^2 + y^2 - |2 * x * y| |
Magnitude Expression

The Magnitude distance metric defines how to compute the magnitude of a point. For example, x^2 + y^2 sums the squares of the x and y coordinates. x^2 simply uses the x coordinate squared and ignores the y coordinate altogether. Each of the above expressions is self-explanatory with the exception of Magnitude Expression. When Magnitude is set to Magnitude Expression, the magnitude is defined by the current Magnitude Expression.

Angle Reference defines the reference point used to form the angle associated with last orbit point. A vector is created from the Angle Reference point to the last orbit point, and the angle between this vector and a horizontal line through the Angle Reference point is saved with the sample data in Sample.AngleRaw.

The Angle Reference is set to one of the following values:

Origin
Previous Orbit Point
Second Previous Orbit Point

Origin (the default) is the origin of the complex plane (i.e., the point 0+0i). Previous Orbit Point is the point prior to current point in the orbit. Second Previous Orbit Point is the point prior to Previous Orbit Point in the orbit.

Bailout and Epsilon are used along with the magnitude described above to terminate the fractal iteration. Divergent fractals terminate the iteration when the magnitude exceeds the Bailout value. Convergent fractals terminate the iteration when the magnitude falls below the value Epsilon. Convergent or Divergent fractals terminate the iteration when either condition occurs.

Min Dwell and Max Dwell define the minimum and maximum number of iterations of the fractal iteration. Min Dwell can be used to force the iteration to execute a minimum number of times and Max Dwell limits the number of iterations to less than or equal to the given value. Min Dwell is rarely changed from its default value of 1. If Process Classic is <Disabled>, Min Dwell and Max Dwell are ignored and the corresponding values given in the Orbit Trap Orbit Generation section are used to define the minimum and maximum number of iterations of the fractal iteration.

Cos Smoothing applies a cosine based smoothing to the magnitude. This tends to introduce a slight rippling effect on the magnitude. This option affects the sample's Magnitude and SmoothingFactor. If Smooth Angle is checked (see below), Cos Smoothing also affects the sample's Angle.

Smooth Angle applies the sample's SmoothingFactor to the sample's Angle to blend the angle across dwells. This is useful when you are using the sample's Angle in the controller and you want to hide the transitions between dwells. Check Cos Smoothing as well to strengthen the effect.

Orbit Trap Orbit Generation

Fractal Science Kit - Mandelbrot / Julia / Newton Properties Orbit Trap Orbit Generation

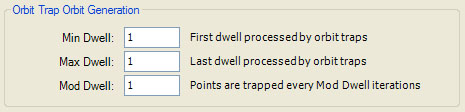
The Orbit Trap Orbit Generation section of the page defines several properties that control when (on which dwells) orbit trap processing takes place. Min Dwell is the 1^st dwell to check for trapped points. Max Dwell is the last dwell to check for trapped points. Mod Dwell - 1 is the number of dwells to skip between checks. That is, a dwell is processed if the dwell is between MinDwell and MaxDwell inclusive, and (dwell - MinDwell) % ModDwell = 0. Min Dwell is used to skip points trapped on the earlier dwells which tend to obscure the later dwells. Max Dwell is used to limit the number of dwells where orbit trap processing is applied, usually for performance reasons. Mod Dwell is used to reduce the dwells where orbit trap processing is applied, usually to cull traps from a busy image. Max Dwell should be less than or equal to the value of Max Dwell given in the Orbit Generation section described above unless Process Classic is <Disabled>.

The default value for both Min Dwell and Max Dwell is 1. This results in processing a single dwell and usually displays the base orbit trap alone on the page. There are two reasons I chose 1 as the default for Max Dwell. First, because some of the orbit traps are complex fractals in their own right (e.g., Kleinian Group, Schottky Group, Apollonian Gasket), they are best displayed outside the context of the Mandelbrot framework. Setting Max Dwell to 1 accomplishes this. Second, several of the orbit traps are very complex geometric objects and using a large value for Max Dwell would result in a fractal that would be too busy and take too long to process. It is best to display each orbit trap alone before you increase the number of iterations so you can get an idea how large or small to make Max Dwell. In addition, you can save some time by playing with the fractal properties when Max Dwell is low so the fractal generation time is fast. Once you find a set of properties resulting in an interesting image, you can increase Max Dwell as required.

Cycle Detection

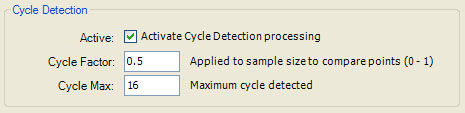
Fractal Science Kit - Mandelbrot / Julia / Newton Properties Cycle Detection

The Cycle Detection section is used to activate/control cycle detection in Divergent fractals. During the iteration of Divergent fractals, points in the Mandelbrot set either converge to a single point or fall into a repeating cycle of points, never to escape. Cycle Detection is the process of checking for these occurrences and terminating the fractal iteration early to improve performance. The Active checkbox is used to activate cycle detection. Cycle Factor is multiplied by the sample point size to obtain a tolerance used when comparing 2 points for equality; points are considered equal if the distance between the points is less than the calculated tolerance. Cycle Max is the largest cycle to check for. Detecting long cycles is more expensive than detecting short cycles. At some point, the cost of cycle detection processing outweighs the benefit. Cycle Max limits the size of the largest cycle to check for, thereby controlling the overall cost.

Cycle Detection introduces visual inaccuracies for inside samples (those samples that are part of the Mandelbrot set). If you are using a controller that maps inside samples to a fixed color (e.g., black), the inaccuracies are hidden. However, if you are using a controller that colors the inside samples based on the sample data, you should disable cycle detection or the visual inaccuracies will appear. Cycle Detection is incompatible with Orbit Trap processing, Convergent fractals, and Root Detection (see below). In each of these cases, Cycle Detection is disabled, even if Cycle Detection is active.

Root Detection

Fractal Science Kit - Mandelbrot / Julia / Newton Properties Root Detection

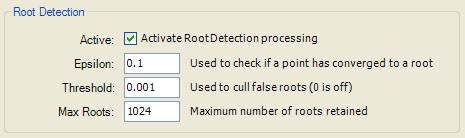
The Root Detection section is used to activate/control root detection processing. Root Detection is the process of detecting points of convergence (called roots) in Julia fractals. It makes no sense to detect roots in Mandelbrot fractals since an infinite number of points of convergence exist, so Root Detection processing is disabled for Mandelbrot fractals even if Root Detection is active.

If Root Detection is enabled, the sample's RootIndexRaw field is set to an index indicating the root to which the sample converged or -1 if the sample failed to converge to a root. The Color Controller can use RootIndexRaw, or the normalized value RootIndex, to map samples that converge to the same root, to the same color.

In Newton fractals (and the other root-finding method fractals), the points of convergence are the roots of the associated equation to which Newton's method is applied, and root detection can be used to color each sample based on the root to which it converged. In fact, Classic Controllers like Gradient Map - Newton do just that; they use the Sample.RootIndex and Sample.RootIndexRaw fields populated by Root Detection to color the fractal.

As stated above, Root Detection is not applicable (and automatically disabled) for Mandelbrot fractals and sample fields Sample.RootIndex and Sample.RootIndexRaw are set to 0 and -1, respectively, for all samples. However, a common approach is to activate Root Detection and use a controller like Gradient Map - Newton to color the Mandelbrot fractal. Then use the Preview Julia feature to explore different Julia fractals by clicking on the Mandelbrot to define the Julia Constant for the preview. The Mandelbrot will be displayed using shades of a single color since Sample.RootIndex is 0 for all samples (the shading is due to 3D processing) but the Julia Preview will be rendered in full color based on the roots found during Root Detection.

In some cases, Divergent Julia fractals can also benefit from root detection processing. For many Divergent Julia fractals, samples associated with points inside the Mandelbrot set (i.e., samples that do not escape) will converge, not to a single point, but to a repeating cycle within the orbit. This same cycle is shared by many of the other samples in the set. When the maximum number of iterations is reached, the current point is arbitrarily taken as the root. Coloring the fractal based on these so-called roots sometimes produces nice results.

Root Detection has 4 associated properties: Active, Epsilon, Threshold, and Max Roots. The Active checkbox activates root detection processing. Epsilon is used to equate a potential root with an existing root. That is, when a potential root is found, if the point is within Epsilon of an existing root, it is taken as the same root. Otherwise, a new root is added to the set of existing roots found thus far. Max Roots limits the number of roots allowed. When we have found Max Roots roots, any new roots are rejected. Threshold is a factor applied to the total number of samples to obtain a minimum number of samples that must converge to a root in order for the root to be accepted. For example, if the total number of samples is 1,000,000 and Threshold is 0.001, then each potential root must meet the criteria that at least 1000 samples (1,000,000*0.001) converge to that root, or the root is taken as a false root and rejected.