
Isogonal Polygon Orbit Trap
Isogonal Polygon is a Fractal Science Kit fractal generator orbit trap based on a construction called an Isogonal Polygon described in:
"Isogonal Decagons" by Branko Grunbaum in the book:
The Pattern Book - Fractals, Art, and Nature
Editor Clifford A. Pickover
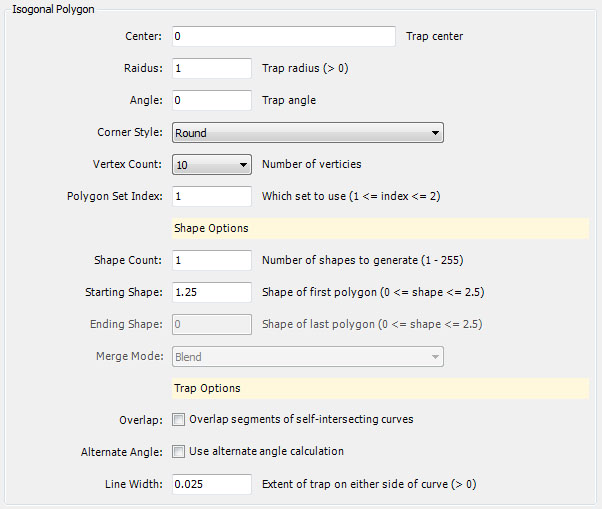
Options are provided to control the Center, Radius, Angle of rotation, style used to display vertices (Corner Style), the number of vertices (Vertex Count), and the index of the set of polygons to use (Polygon Set Index). Vertex Count is a number in the form 4*M+2 for some integer M. Polygon Set Index is an integer in the range 1 to M. Polygon Set Index represents a group of polygons with Vertex Count vertices where the shape of each polygon is controlled by a shape control value S which ranges 0 to Vertex Count / 4. Some of the polygons may appear to have less than Vertex Count vertices if some of the vertices have the same coordinates.
The Shape Options section has 4 properties: Shape Count, Starting Shape, Ending Shape, and Merge Mode. Shape Count is the number of polygons to generate. Starting Shape and Ending Shape are the shape control values described above for the first and last polygon. The shape control values for the remaining polygons are determined by linear interpolation between Starting Shape and Ending Shape. The trapped point's Index is set to a value between 0 and Shape Count - 1 and is the index of the polygon that trapped the point.
Merge Mode controls how the polygons are positioned relative to one another and is one of the following: Blend, New Above, or New Below. If Merge Mode is Blend, the set of polygons are blended into a single curve. If Merge Mode is New Above, the new polygons are placed above the existing polygons. If Merge Mode is New Below, the new polygons are placed below the existing polygons.
See Trap Options for a description of the remaining options.
See also: