
Transfer Function Overview
A Fractal Science Kit fractal generator Transfer Function can be applied to data to accentuate one area within the data while minimizing another. A Transfer Function is used to support Data Normalization and other processing tasks throughout the application where remapping data in the interval 0 to 1 is required.
Transfer Function is one of the following:
- Linear
- Log
- Inverted Exp
- Root
- Inverted Power
- Inverted Elliptic
- Elliptic
- Power
- Inverted Root
- Exp
- Inverted Log
- Sigmoid
- Inverse Sigmoid
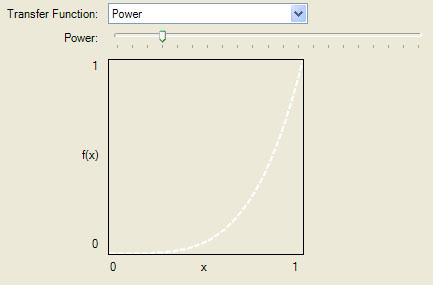
The Linear function is the identity transformation. The rest of the functions remap data in the interval 0 to 1. The shape of the map is based on the named function. All of the functions, with the exception of Linear, take a Power argument which controls the strength of the function applied to each data value.
Select a Transfer Function from the set of functions and use the Power slider to adjust the power. The transfer function/power graph shows how the data is remapped by the selected function/power. For each x value on the horizontal axis, the graph shows the associated value of f(x) on the vertical axis, where f(x) is the chosen function/power.
Each function is defined such that f(x)=x for x=0 or x=1. The values between 0 and 1 however are scaled up/down based on the function type and power. For example, the Root function with Power set to 2 would be f(x)=Sqrt(x) and would scale up values between 0 and 1.