
In Part 8 of the tutorial, we are going to try out a Classic Controller related to the Magnitude distance metric y^2.
Select the Fractal Equation: Mandelbrot properties page:
General
Mandelbrot / Julia / Newton
Fractal Equation: Mandelbrot
This page is a Program Editor for the Fractal Equation.
Change the Based On property to Trig 14.

The Fractal Equation sets the Magnitude distance metric to y^2 in the global section of the instructions. Normally, you would set the Magnitude distance metric in the Orbit Generation section of the Mandelbrot / Julia / Newton page but this equation uses FSK.OverrideValue to set it in the code.
Now, return to the controller's page and change the Based On property to Gradient Map - Angle Relief (y^2).

Read the comments in the program's Instructions at the bottom of the page. The comments give you a description of what the program does and how to use the program's properties page found below the controller in the hierarchy (usually called Properties).
Select the program's Properties page and change Color Scheme to 4 Colors - Gold, Silver, Bronze, Silver.

Now, execute the Resize command on the View menu of the Fractal Window to display the Set Image Viewport dialog.
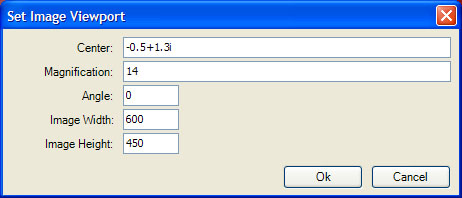
Set Center to -0.5+1.3i and Magnification to 14 and click Ok and wait while the application generates the sample data and processes the fractal image shown below.
This controller generates what looks like plant life, scales, or feathers. At each dwell, a number of finger like structures protrude from the previous dwell's fingers. The number of these protrusions is proportional to the Bailout (see Orbit Generation). You can increase/decrease the Bailout to create more/less protrusions. Bailout should be 256 or less for the best results.
Now, scroll down near the bottom of the page to the 3D Mapping section and check Apply Depth.
![]()
Execute the Display Fractal command on the Tools menu of the Fractal Window to generate the fractal image.
This gives the image a metallic quality.
This concludes the Mandelbrot fractal tutorial. Click <Next> to continue with the Orbit Traps Tutorial.

