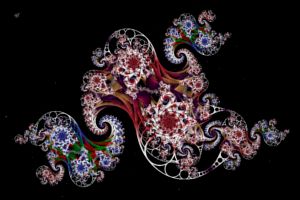
Steiner Chain Orbit Trap Examples
The Steiner Chain Orbit Trap examples apply a Steiner Chain Orbit Trap to a fractal based on various Fractal Equations.
Note the following:
| Example | Fractal Type | Fractal Equation |
| Steiner Chain Orbit Trap 01 | Mandelbrot Fractal | Mandelbrot |
| Steiner Chain Orbit Trap 02 | Mandelbrot Fractal | Mandelbrot |
| Steiner Chain Orbit Trap 03 | Mandelbrot Fractal | Mandelbrot |
| Steiner Chain Orbit Trap 04 | Mandelbrot Fractal | Mandelbrot |
| Steiner Chain Orbit Trap 05 | Mandelbrot Fractal | Mandelbrot |
| Steiner Chain Orbit Trap 06 | Mandelbrot Fractal | Mandelbrot |
| Steiner Chain Orbit Trap 07 | Mandelbrot Fractal | Mandelbrot |
| Steiner Chain Orbit Trap 08 | Mandelbrot Fractal | Mandelbrot |
| Steiner Chain Orbit Trap 09 | Mandelbrot Fractal | Mandelbrot |
| Steiner Chain Orbit Trap 10 | Mandelbrot Fractal | Mandelbrot |
| Steiner Chain Orbit Trap 11 | Mandelbrot Fractal | Mandelbrot |
| Steiner Chain Orbit Trap 12 | Mandelbrot Fractal | Mandelbrot |
| Steiner Chain Orbit Trap 13 | Mandelbrot Fractal | Mandelbrot |
| Steiner Chain Orbit Trap 14 | Julia Fractal | Exp 15 |
| Steiner Chain Orbit Trap 15 | Julia Fractal | Trig 4 |
| Steiner Chain Orbit Trap 16 | Julia Fractal | Trig 4 |
| Steiner Chain Orbit Trap 17 | Julia Fractal | Exp 6 |
| Steiner Chain Orbit Trap 18 | Julia Fractal | Exp 6 |
| Steiner Chain Orbit Trap 19 | Julia Fractal | Exp 6 |
| Steiner Chain Orbit Trap 20 | Julia Fractal | Trig 4 |
| Steiner Chain Orbit Trap 21 | Julia Fractal | Trig 4 |
| Steiner Chain Orbit Trap 22 | Julia Fractal | Trig 4 |
| Steiner Chain Orbit Trap 23 | Julia Fractal | Trig 4 |
| Steiner Chain Orbit Trap 24 | Julia Fractal | Trig 4 |
| Steiner Chain Orbit Trap 25 | Mandelbrot Fractal | Mandelbrot |
| Steiner Chain Orbit Trap 26 | Mandelbrot Fractal | Mandelbrot |
| Steiner Chain Orbit Trap 27 | Mandelbrot Fractal | Mandelbrot |
In the remaining sections, when I refer to the equation, I will use Trig 4, but you should use the equation for the example you are working with.
Zoom In/Out
Zoom In or Zoom Out to examine different parts of the fractal.
Execute the Home command on the View menu of the Fractal Window to reset the fractal to the default position/magnification, and then Zoom In to other areas.
Remember that as you Zoom In, you may need to increase the Max Dwell property found in the Orbit Trap Orbit Generation section of the General page.
Explore the Julia Fractals
For the Mandelbrot Fractal examples, you can use the Preview Julia command to explore the Mandelbrot's many different Julia Fractals. This is a common technique that can be used to generate lots of different Julia fractals from a single Mandelbrot image.
Execute the Home command on the View menu of the Fractal Window to reset the Mandelbrot fractal to the default position/magnification, and use the Preview Julia command to explore the Mandelbrot's many different Julia Fractals. See Working with Julia Fractals for details.
Change the Julia Constant
For the Julia Fractal examples, you can generate other Julia Fractals based on the same equation.
Select the Fractal Equation:
General
Mandelbrot / Julia /
Newton
Fractal Equation: Trig 4
Uncheck the Julia checkbox, execute the Home command on the View menu of the Fractal Window to reset the Mandelbrot fractal to the default position/magnification, and use the Preview Julia command to explore the Mandelbrot's many different Julia Fractals. See Working with Julia Fractals for details.
Alternatively, you can change the Julia Constant property on the Fractal Equation page, and then click the Preview Fractal toolbar button on the Properties Window to generate a preview of your change in the Preview Window.
Change the Fractal Equation
You can change the Fractal Equation used to generate the fractal.
Select the Fractal Equation:
General
Mandelbrot / Julia / Newton
Fractal Equation: Trig 4
Change the Based On property to one of the other Fractal Equations.
Then execute the Home command on the View menu of the Fractal Window to reset the Mandelbrot fractal to the default position/magnification, and use the Preview Julia command to explore the Mandelbrot's many different Julia Fractals. See Preview Julia Support for details.
Remember to navigate to the properties page for the equation (found under the equation in the page hierarchy) and play with the different properties found there. Many of the equations support properties that can be used to generate lots of different variations.
Change the Steiner Chain Properties
Change the Steiner Chain orbit trap properties.
Select the orbit trap's properties page:
General
Mandelbrot / Julia / Newton
Orbit
Trap
Orbit Trap Map
Instructions: Steiner Chain
Properties
Change the Steiner Circle Options properties to change the orbit trap.
Change the Orbit Trap
You can try out different Orbit Traps.
Select Instructions: Steiner Chain:
General
Mandelbrot / Julia /
Newton
Orbit
Trap
Orbit Trap Map
Instructions: Steiner Chain
Change the Based On property to one of the following Orbit Traps:
- Circle
- Line
- Polygon
- General Polygon
- Shape
- Sphere
- Patterned Sphere
- Solid Polygon
- Solid General Polygon
- Patterned Polygon
- Patterned General Polygon
- Epicycloid Polygon
- Hypocycloid Polygon
- Cross
- Crossed Lines
- Image
- Cassinian Curve
- Limacon
- Lemniscate
- Folium
- Cycloid of Ceva
- Circular Vine
- Celtic Knot
- Borromean Rings
- Tangent Circles
- Steiner Chain
- Rep-4 Tile
- Rep-4 Tile Patterned Polygon
- Rep-4 Tile Patterned General Polygon
- Rep-9 Tile
- Rep-9 Tile Patterned Polygon
- Rep-9 Tile Patterned General Polygon
- Polygon Motif
- Star of David
- String of Beads
- Wheel
- Ornament
- Sectors
- Triangles
- Star Polygon
- Faceted Polygon
- Composite Shape
- Spiral
- Daisy
- Swirl
- Flower
- Rose
- Super Ellipse
- Shapes
- Squares
Each of these programs have properties (on the properties page found under the orbit trap) to manipulate the trap and thereby change the resulting fractal. There are several orbit traps not given in the above list since they are stand-alone fractals or are too complex to display in this context.
You can also try out the different optimized orbit traps. To do this, select Orbit Trap Map:
General
Mandelbrot / Julia /
Newton
Orbit
Trap
Orbit Trap Map
Change the Type property to one of the following:
- Circle
- Cross
- Epicycloid
- Fractal Gasket
- Gear
- Hypocycloid
- Isogonal Polygon
- Koch Triangle
- L-System
- Oscillator
- Penrose Kite
- Polygon
- Rectangle
- Rose
- Shape
- Sierpinski Triangle
- Spirolateral
- Star Polygon
- Triangle
Each of these orbit traps have properties (on the page found under the Orbit Trap Map page) to manipulate the trap and thereby change the resulting fractal.
Change the Transformation
You can apply a transformation to the initial orbit point, or to each orbit point prior to passing it to the orbit trap.
Execute the Home command on the View menu of the Fractal Window to reset the fractal to the default position/magnification before you adjust the transformation. Then change the transformation and Zoom In to interesting areas of the transformed image.
To change the transformation applied to the initial orbit point, select the transformation's properties page:
General
Mandelbrot / Julia / Newton
Transformation
Composite
Function
Properties
Set the F(z) property to one of the complex functions in the list. You can change some of the other properties on this page for more variations.
You can also use a different transformation altogether. Select the Composite Function page, and change the Based On property to select a transformation and then open the transformation's properties page (found under the transformation in the page hierarchy), and play with the transformation's properties. See Transformation Support for details.
Note that some of the examples are set to the Identity transformation rather than the Composite Function transformation:
General
Mandelbrot / Julia / Newton
Transformation
Identity
For those examples, select the Identity page and change the Based On property to select a transformation and then open the transformation's properties page (found under the transformation in the page hierarchy), and play with the transformation's properties. See Transformation Support for details.
To change the transformation applied to each orbit point prior to passing it to the orbit trap, select the transformation's properties page:
General
Mandelbrot / Julia / Newton
Orbit
Trap
Transformation 1
Composite Function
Properties
Set the F(z) property to one of the complex functions in the list. You can change some of the other properties on this page for more variations.
You can also use a different transformation altogether. Select the Composite Function page, and change the Based On property to select a transformation and then open the transformation's properties page (found under the transformation in the page hierarchy), and play with the transformation's properties. See Transformation Support for details.
Note that some of the examples are set to the Identity transformation rather than the Composite Function transformation:
General
Mandelbrot / Julia / Newton
Orbit
Trap
Transformation 1
Identity
For those examples, select the Identity page and change the Based On property to select a transformation and then open the transformation's properties page (found under the transformation in the page hierarchy), and play with the transformation's properties. See Transformation Support for details.