Blended Value

Home • Gallery • Tutorials • Download • Purchase • Site Map

Alternate Mapping: Blended Value

The Fractal Science Kit fractal generator Alternate Mapping Blended Value returns the blended value over all points P in each orbit. A shape transformation is applied to each orbit point at the beginning of each iteration.

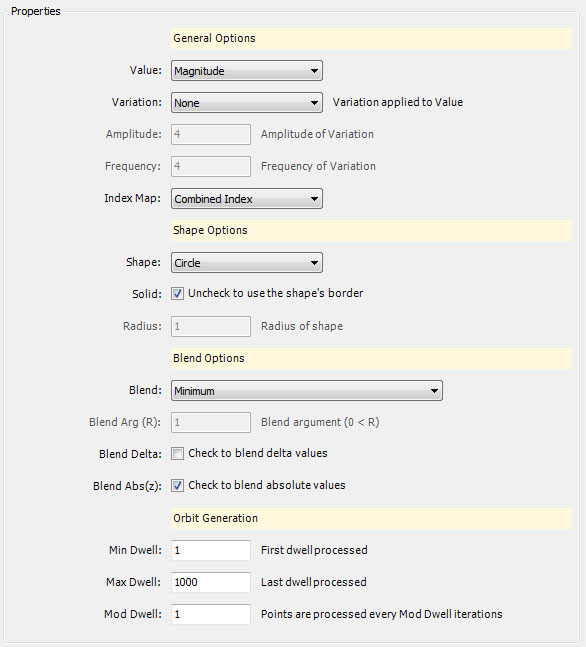
General Options

The Value property controls which values to process. Value is one of:

Magnitude
Orbit Transformation
Triangle Metric

Magnitude is given by the Magnitude property on the Mandelbrot / Julia / Newton page. Orbit Transformation is defined by the Orbit Transformation page. Triangle Metric is defined by the Triangle Metric page. Like P, the Previous Point and the Second Previous Point are based on the selected Value. For example, if Value is Triangle Metric, P is the Triangle Metric point and the Previous Point is the previous Triangle Metric point.

Variation is one of:

None
Angular Wave
Angular Bounce
Radial Wave
Radial Bounce
Horizontal Wave
Horizontal Bounce
Vertical Wave
Vertical Bounce
XY Wave
XY Bounce

Variation sets the wave/bounce transformation applied to the value. The amplitude/frequency of the wave/bounce are given by the Amplitude and Frequency properties. Both properties can be positive or negative but not 0.

Index Map controls the value of the alternate point's Index.

Shape Options

The Shape Options section allows you to control the shape transformation applied to each orbit point at the beginning of each iteration.

Shape defines the shape associated with the shape transformation applied to the value.

If Solid is checked, the shape transformation is based on a solid shape. Otherwise, the transformation is based on the border of the shape.

Radius defines the radius of the shape and is only important if the shape is not solid.

Blend Options

The Blend Options section controls the strategy employed to blend the set of orbit point values into a single value.

Blend can be one of the following values:

Minimum
Sum
Product
Power Mean: -2
Power Mean: -1 (Harmonic Mean)
Power Mean: 0 (Geometric Mean)
Power Mean: 1 (Arithmetic Mean)
Power Mean: 2 (Quadratic Mean)
Lehmer Mean: -2
Lehmer Mean: -1
Lehmer Mean: 0 (Harmonic Mean)
Lehmer Mean: 1 (Arithmetic Mean)
Lehmer Mean: 2 (ContraHarmonic Mean)
Generalized Mean: f(x) = (x+R)/(x-R)
Generalized Mean: f(x) = (R-x)/(x+R)
Generalized Mean: f(x) = 1/(R+x)+1/(R-x)
Generalized Mean: f(x) = x/(R+x)-x/(R-x)
Generalized Mean: f(x) = Sin(R*x)
Generalized Mean: f(x) = Cos(R*x)
Generalized Mean: f(x) = Tan(R*x)
Generalized Mean: f(x) = Cot(R*x)
Generalized Mean: f(x) = Sec(R*x)
Generalized Mean: f(x) = Csc(R*x)
Generalized Mean: f(x) = Sinh(x)
Generalized Mean: f(x) = Csch(x)
Generalized Mean: f(x) = Log(x)
Generalized Mean: f(x) = Exp(x)
Variance

The simplest (and default) Blend is Minimum. This uses the minimum value of all the orbit points. Sum and Product simply return the sum and product of the values, respectively. The Power Mean, Lehmer Mean, and Generalized Mean settings return the named mean. Variance returns the variance. The symbol R in some of the names above indicates the blend algorithm requires an argument which is given by Blend Arg (R).

If Blend Delta is checked, the blend is applied to the absolute value of the difference between each point and its predecessor.

For details about Power Mean, Lehmer Mean, or the Generalized Mean, see the following:

Eric W. Weisstein. "Power Mean."

From MathWorld--A Wolfram Web Resource.

Eric W. Weisstein. "Lehmer Mean."

From MathWorld--A Wolfram Web Resource.

"Generalized mean."

From Wikipedia, the free encyclopedia.

Orbit Generation

The Orbit Generation section defines 3 properties: Min Dwell, Max Dwell, and Mod Dwell. These values control the set of orbit points that are considered when processing the orbit. Min Dwell is the 1^st dwell to check. Max Dwell is the last dwell to check. Mod Dwell - 1 is the number of dwells to skip between checks. That is, a dwell is processed if the dwell is between MinDwell and MaxDwell inclusive, and (dwell - MinDwell) % ModDwell = 0.